ラティスが実現する機械的特性の向上
3Dプリントにより、従来の製造プロセスでは作成が困難または不可能なさまざまな形状のモノづくりが可能になります。特にラティスは、より優れた圧縮およびエネルギー吸収特性を持つ部品から軽量部品まで、望ましい機械的特性の世界を切り開いてきました。
一般的な使用例としては、標準のフォームパッドをより優れた剛性対質量比を持つラティスへ置き換えや、優れたエネルギー吸収特性を持つラティスを使用したヘルメットや自動車シートなどの保護用具の改善があります。
Carbonの計算幾何学チームは、従来のストラット(支柱)ベースのラティスと新しいサーフェイスラティス(表面格子)の広大なパラメータ空間を調査しました。このパラメータ空間を探索することによりラティス設計の革新が促進され、消費財の剛性とエネルギー吸収に対する新しい限界が明らかになりました。
その発見プロセスに光を当てるために、サーフェイスラティスの幾何学的構造を支える数学と工学のいくつか、そして部品が完成品に至るまでに受ける関連分析について説明します。
最先端の機械的特性を備えたラティス製品
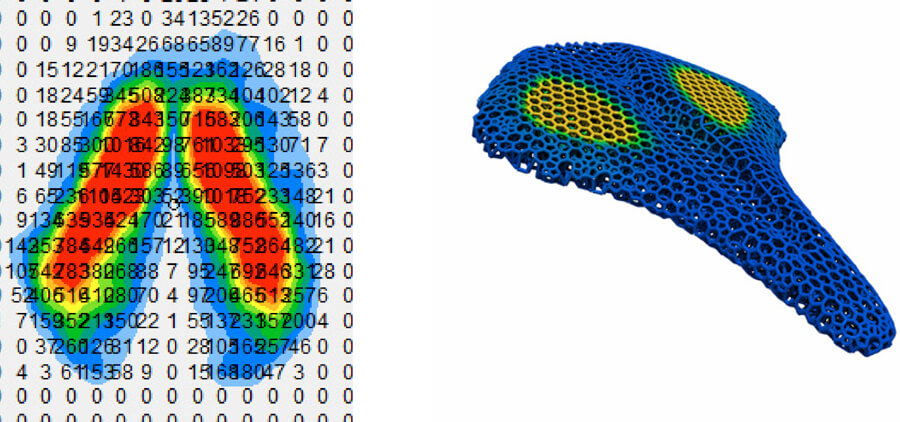
座骨の快適性のために設計された、適応的な反発力分布を有するバイクサドル。Specialized S-Worksパワーサドルの詳細については、こちらをご覧ください。

エネルギー吸収のために設計されたリデルヘルメットと、エネルギー反発のために設計されたアディダスシューズ。Carbonラティス製品の詳細については、こちらをご覧ください。
サーフェイスラティスの宇宙
等高線による迂回路:2次元等高線図
いわゆる「サーフェイスラティス」は、おなじみの2次元等高線図を3次元に拡張したものです。等高線図では、2次元の各等高線は関数の「等値」に対応します。
つまり関数はある等高線上のすべての点で同じ(「等」)値を取るということです。たとえば、関数g(x、y)= cos(x)+ cos(y)について考えてみます。左下のプロットは、等値g(x、y)= 0.5の等高線を示しています。次に不等式| g(x、y)|<0.5をプロットすると、等高線内側の塗りつぶされた領域を示します(右下)。
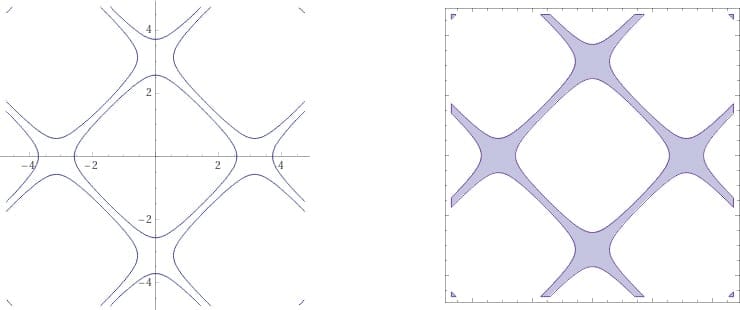
2次元等高線から3次元等体積へ
その等高線を2次元から3次元に拡張すると、等高線の代わりに等値面が得られ、面内のスペースを埋めると3次元体積が生成されます。
上述の関数g(x、y)を3次元に拡張すると、シュワルツPタイプラティスとして知られ、広く研究されているサーフェイスラティス(「等容積」とも呼ばれます)を定義する関数が得られます。
ここに描かれているのは、関連する関数g(x、y、z)= cos(x)+ cos(y)+ cos (z)が不等式| g(x、y、z)| <tを満たすような、立法体グリッド[-π、π] 3内の点のセットを取得することによって生成されたシュワルツの単一セルです。

これらのユニットセルの複数のコピーを一緒に並べて、3次元モデルを埋めるために任意の形状とサイズのラティスを構築することができます。

製品に使用される一般的なラティス
これらのサーフェイスラティスは、さまざまな用途に適した圧縮特性と剛性対質量比を実現します。シュワルツラティスの興味深い座屈挙動により、クッションが必要な用途に適した材料となりますが、一方で他の一般的なサーフェイスラティスであるジャイロイドは、その高エネルギー吸収性により多くの保護パッドの基本骨格となります。

ジャイロイドラティス

リデルのヘルメットと、ジャイロイドラティス内部に格子状の支柱による外層を備えたパッド。
高次パラメータ領域を通じた移行
アプリケーションは常に、目前のタスクに合わせてカスタマイズされた機械的特性を備えるラティスから、さらなる恩恵を受けることができます。
アプリケーション固有のニーズを満たすためにさらに高度に専門化されたラティスを特定するために、Carbonエンジニアは、シュヴァルツラティスとジャイロイドラティスを定義する等体積関数の一般化された形式を最適化するべく取り組んでいます。
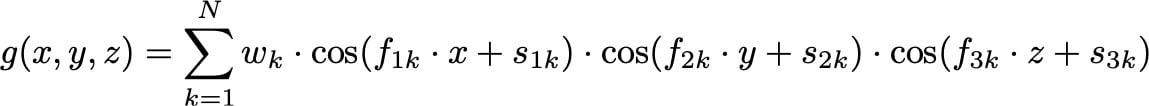
この一般的な形式の重量(wk)、周波数(fjk)、および位相シフトパラメーター(sjk)を調整することにより、既知のラティスのハイブリッドを生成し、より具体的に最適化された力のプロファイルに焦点を絞ることができます。
たとえば、1つの軸に沿って剛性が高いシュワルツラティスの相対値を作成するために、シュワルツの関数を、その方向の剛性が調整されたラティスの関数と組み合わせることができるのです。

カスタムラティスを作成するには、いくつかの適切なラティスの定義パラメータを取得し、それらを混合して目的の特性を実現します。変化するパラメータは、あるサーフェイスラティスから次のサーフェイスラティスへと連続的にスムーズに移行し、本質的に無限のラティス候補を提示します。

十分に膨大なラティスを生成したらこのデータベースを整理および検索して、潜在的に興味深く且つ有用な新しい機械的挙動を発現させる、有望なラティスの微調整バージョンを見出すことができます。ラティスデータベースのあるバージョンで見つけ出した、シュワルツP近傍のいくつかは以下のようなものです。

ラティスを評価する
探索した無数のパラメータの組み合わせから、さらなる評価を行うためのサブセットを手動で選択し、シミュレーションソフトウェアの実行によって剛性やエネルギー吸収などの機械的挙動をより理解するようにします。
 圧縮シミュレーター上の、シュワルツの混合変形版 |
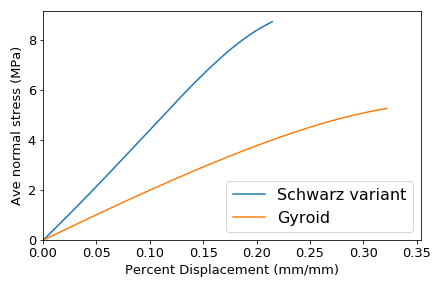 圧縮シミュレーターを介して実行されているシュワルツの混合変形版の応力-ひずみ曲線は、同等の質量のジャイロイドラティスと比較して大幅に高い初期剛性を示しています。 |
最も有望なラティスはシミュレーションでは十分に対応できず、実際のハードウェアを使用したプリントとテストが必要となります。これによって、剛性とエネルギーの吸収性および反発性を測定し、例えば「ラティスクッションは高衝撃打撃をどのくらい吸収するのか?」というようなアプリケーション固有の質問に答えることができるようになるのです。
 一定の荷重および一定の高さからの落下条件の場合に、ジャイロイドパックを介して伝達される力を圧縮装置で測定。 |
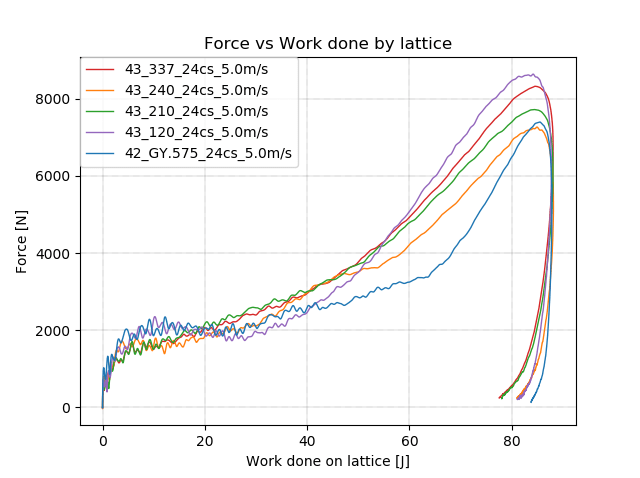 グラフは、いくつかの異なるラティスを介して伝達されるピーク力を示しています。低いピーク力で一定量のエネルギーを吸収するパックは、保護用具の有望な候補となります。 |
最高のパフォーマンスを発揮するパックは、個々の製品ごとに実験が継続されています。このR&Dプロセスを経たCarbonラティスを搭載したリデルのSpeedflexヘルメットは、2020年のNFLテストチャートを上回る衝撃低減性能を実現しました。

まとめ
サーフェイスラティスの領域は、保護用具や運動器具から医療用品まで、パフォーマンスの新しい可能性を開く無限で多様な機械的特性を内包しています。このパラメータの世界を探索すると、複雑で学際的な問題が多く発生します。
ラティス領域での新しい局所最適点の発見は、最先端の製品につながる可能性があり、ひいてはより良い性能と優れた器具を意味することになるのです。
